Research in the Manning group follows two interconnected thrusts: Collective behavior in biological tissues and deformation in disordered solids. Click sub-topic headings below for additional detail.
Geometric Signature Of Surface Tension In 3D Tissues Collaborators: Simulating The Mechanical Coupling Between A Tumor And Its Extracellular Matrix Environment Collaborators: Morphogen Gradients Inside Active Confluent Tissue – – Organogenesis During Development Collaborators: Mechanisms For Compartmentalization And Cell Sorting In Biological Tissues Collaborators: Rigidity In Confluent 3D Bulk Tissues And The Origin Of Rigidity In Vertex Models Collaborators: Flocking And Pattern Formation In Confluent Tissues Collaborators: Predicting Crowd Dynamics Using Local Structure – – Structural Evolution Of Amorphous Systems During Large Scale Deformation – – Jammed Packings Under A Random Force Collaborators: What Are The Distinct Mechanically Stable States In Jammed Solids? Collaborators: Collaborators: Collaborators:
Groups of cells exhibit interesting collective behavior that emerges from simple interactions between individual cells. We search for universal features and rules that govern this far-from-equilibrium behavior.
Manning group participants:
• Elizabeth Lawson-Keister
• Preeti Sahu
• Jennifer Schwarz (SU)
• Lisa Manning
• Carien Niessen
• Matthias Rubsam
Manning group participants:
• Tara Finnegan
• Amanda Parker
• Jen Schwarz (SU)
• Lisa Manning (SU)
• Cristina Marchetti (UCSB)
Manning group participants:
• Elizabeth Lawson Keister
–
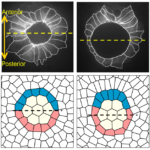Manning group participants:
• Paula Sanematsu
• Gonca Erdemci-Tandogan
• Matthias Merkel
• Jeff Amack (SUNY Upstate)
• Agnik Dasgupta (SUNY Upstate)
Manning group participants:
• Daniel Sussman
• Preeti Sahu
• Jen Schwarz (SU)
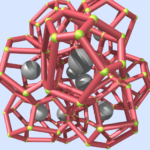Manning group participants:
• Matthias Merkel
• Daniel Sussman
• Josef Käs, Andrea Liu and Tristan Sharp (U Penn)
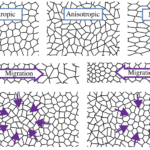Manning group participants:
• Michael Czajkowski
• Max Dapeng Bi
• Matteo Paoluzzi (SU)
• Cristina Marchetti (SU)
• Fabio Giavazzi, Giorgio Scita, and Roberto Cerbino (Milano)
If you push a pile of sand very lightly, it will respond elastically, but if you push beyond an extremely low threshold, it will begin to flow. But the system that it flows into will be qualitatively similar to the state it was just in. We are studying that marginal transition in low dimensional systems (2D and 3D):
Manning group participants:
• Julia Giannini
• Ethan Stanifer
Manning group participants:
• Ethan Stanifer
_
Manning group participants:
• Sudeshna Roy
• Ethan Stanifer
• Lisa Manning
• Peter Morse
Manning group participants:
• Peter Morse
• Sven Wijtmans
• Martin Van Hecke
• Merlijn Van Deen (Leiden)
Modeling Jammed Solids with Sparse Random Matrices
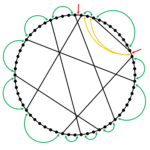Manning group participants:
• Ethan Stanifer
• Peter Morse
• Alan Middleton (SU Physics)
Identifying Low-Frequency Excitations In Jammed Systems
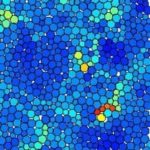Manning group participants:
• Ethan Stanifer
• Peter Morse
• Sven Wijtmans
• Alan Middleton (SU Physics)
• Eric Corwin (U Oregon)