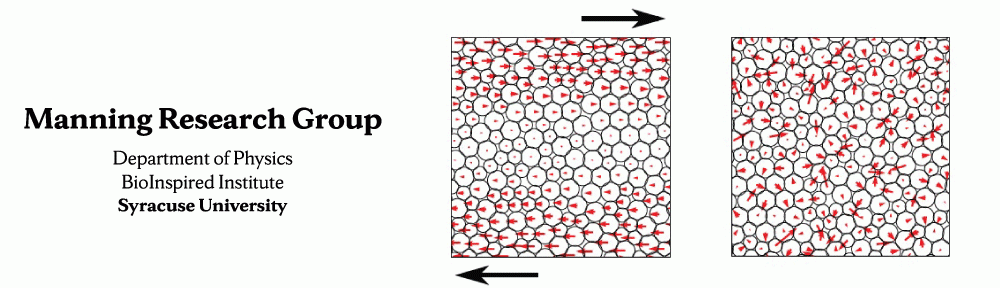
Surface tension governed by differential adhesion can drive fluid particle mixtures to sort into separate regions, i.e., demix. Does the same phenomenon occur in confluent biological tissues? We begin to answer this question for epithelial monolayers with a combination of theory via a vertex model and experiments on keratinocyte monolayers. Vertex models are distinct from particle models in that the interactions between the cells are shape-based, as opposed to distance-dependent. We investigate whether a disparity in cell shape or size alone is sufficient to drive demixing in bidisperse vertex model fluid mixtures. Surprisingly, we observe that both types of bidisperse systems robustly mix on large lengthscales. On the other hand, shape disparity generates slight demixing over a few cell diameters, a phenomenon we term micro-demixing. This result can be understood by examining the differential energy barriers for neighbor exchanges (T1 transitions). Experiments with mixtures of wild-type and E-cadherin-deficient keratinocytes on a substrate are consistent with the predicted phenomenon of micro-demixing, which biology may exploit to create subtle patterning. The robustness of mixing at large scales, however, suggests that despite some differences in cell shape and size, progenitor cells can readily mix throughout a developing tissue until acquiring means of recognizing cells of different types.

https://pubs.rsc.org/en/Content/ArticleLanding/2020/SM/C9SM01084J#!divAbstract

The fluidity of biological tissues – whether cells can change neighbors and rearrange – is important for their function. In traditional materials, researchers have used linear response functions, such as the shear modulus, to accurately predict whether a material will behave as a fluid. Similarly, in disordered 2D vertex models for confluent biological tissues, the shear modulus becomes zero precisely when the cells can change neighbors and the tissue fluidizes, at a critical value of control parameter s₀* = 3.81. However, the ordered ground states of 2D vertex models become linearly unstable at a lower value of control parameter (3.72), suggesting that there may be a decoupling between linear and nonlinear response. We demonstrate that the linear response does not correctly predict the nonlinear behavior in these systems: when the control parameter is between 3.72 and 3.81, cells cannot freely change neighbors even though the shear modulus is zero. These results highlight that the linear response of vertex models should not be expected to generically predict their rheology. We develop a simple geometric ansatz that correctly predicts the nonlinear response, which may serve as a framework for making nonlinear predictions in other vertex-like models.

https://pubs.rsc.org/en/content/articlelanding/2020/sm/c9sm01068h#!divAbstract

Work done by undergraduate SBI REU student Janice Kang and her graduate mentor Preeti Sahu on quantifying the nature of the rigidity transition in models for ordered biological tissues – ‘Non-linear analysis of the fluid-solid transition in a model for ordered biological tissues’ by Preeti Sahu, Janice Kang, Gonca Erdemci-Tandogan and M. Lisa Manning is now posted on ArXiv.

arXiv:1905.12714v1